MATEMÁTICA - 3ª SEMANA - PROF: STENIO AGUIAR - 7ª A - CORREÇÃO DE FLUXO

MATEMÁTICA – 3ª SEMANA

ANO/SEGMENTO: 7º Ano/ CORREÇÃO DE FLUXO
COMPONENTE CURRICULAR: Matemática 
UNIDADES TEMÁTICAS: Números

OBJETOS DE CONHECIMENTO:

1. Múltiplos e divisores de um número natural;
2. Cálculo de porcentagens e de acréscimos e decréscimos simples.

HABILIDADES:

(EF07MA01) Resolver e elaborar problemas com números naturais, envolvendo as noções de divisor e de múltiplo, podendo incluir máximo divisor comum ou mínimo múltiplo comum, por meio de estratégias diversas, sem a aplicação de algoritmos.

(EF07MA02) Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros.

DESENVOLVIMENTO DO PLANO:

 Múltiplos e divisores de um número natural:

 LINKS PARA ESTUDAR OS MÚLTIPLOS E DIVISORES DE UM NÚMERO NATURAL:

• https://www.youtube.com/watch?v=MVxkuFoRSgc

• https://www.youtube.com/watch?v=S5PhiSHK01E

• https://www.youtube.com/watch?v=-DxJXs_yP9s

• https://www.youtube.com/watch?v=Jo95HkmPgwA

• https://www.youtube.com/watch?v=Nkt-2zox1zE 

   

LINKS PARA ESTUDAR MMC E MDC DE NÚMEROS NATURAIS:

• https://www.youtube.com/watch?v=t6rvMRGrEr0

• https://www.youtube.com/watch?v=Ao7Sz3gdmNY 

• https://www.youtube.com/watch?v=dqT7zHoMmjQ

• https://www.youtube.com/watch?v=32KlYtaouPA 

   

  MÚLTIPLOS E DIVISORES DE UM NÚMERO NATURAL:

  Múltiplos e Divisores de um número é o conjuntos formado por números que são múltiplos ou divisores deste número.
  
  Múltiplos são números que resultam da multiplicação de um número qualquer por qualquer qualquer número natural.
  
  Os divisores de um número natural são os números que usamos na multiplicação desse número por outro número natural.
  
  

  Múltiplos de um número natural:

  Para descobrir os múltiplos de um número podemos seguir a seguinte ideia: pegar esse número e multiplicar pelos números naturais.
  
  O conjunto dos múltiplos de um número é infinito.
  
  Conjuntos dos números naturais: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …}
  
  Exemplos:
  
  Múltiplos de 2
  
  Os múltiplos de 2 são quaisquer números que resultam da multiplicação por 2.
• 2 x 0 = 0
• 2 x 1 = 2
• 2 x 2 = 4
• 2 x 3 = 6
• 2 x 4 = 8
• 2 x 5 = 10
• 2 x 6 = 12
• 2 x 7 = 14
• 2 x 8 = 16
• 2 x 9 = 18
• 2 x 10 = 20

Dessa forma, 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 e 20 são múltiplos de 2. Os múltiplos de 2 são sempre pares. Perceba que começando com o zero os números foram acrescidos de 2.
Além disso, todos esses números são divisíveis por 2, ou seja, um número que é múltiplo de 2 também é divisível por 2.

Veja alguns múltiplos de 3, 4, 5, 6, 7, 8, 9 e 10:

• Múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, …
• Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24, 28, …
• Múltiplos de 5: 0, 5, 10, 15, 20, 25, 30, 35, …
• Múltiplos de 6: 0, 6, 12, 18, 24, 30, 36, …
• Múltiplos de 7: 0, 7, 14, 21, 28, 35, 42, …
• Múltiplos de 8: 0, 8, 16, 24, 32, 40, 48, …
• Múltiplos de 9: 0, 9, 18, 27, 36, 45, 54, …
• Múltiplos de 10: 0, 10, 20, 30, 40, 50, …

12 é múltiplo de 6, pois 6 x 2 é igual a 12. Veja na imagem:

Conseguimos agrupar 12 em dois grupos de 6, isso explica também porque 12 é divisível por 6, porque conseguimos dividir 12 em 2 grupos de 6.


A tabuada de multiplicação é formada pelos múltiplos de um número natural. 

Divisores de um número natural:

Podemos dizer que os divisores de um número são quaisquer números que divididos por ele tem resto zero, divisão exata.

Exemplo:

Dizemos que 10 é divisível por 2 ou 2 é divisor de 10, pois 10 dividido por 2 é 5, uma divisão exata.

Se 12 é divisível por 3, assim 3 é divisor de 12, portanto 12 é múltiplo de 3.

Veja na imagem que ao dividirmos 12 por 3 temos uma divisão exata, ou seja, não sobra nada. Conseguimos dividir 12 em 4 partes iguais.

Agora veja que 12 não é divisível por 5, pois não temos uma divisão exata, ou seja, sobra dois, tem resto 2. Não conseguimos dividir 12 em partes iguais.

O conjunto dos divisores de um número é sempre finito e menor que este número.

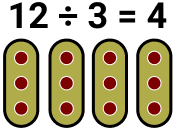
Exemplo:

• Conjuntos dos divisores de 12: 1, 2, 3, 4, 6 e 12.
• Conjuntos dos divisores de 50: 1, 2, 5, 10, 25 e 50

 

MMC E MDC DE NÚMEROS NATURAIS:

Você já observou como o cálculo do Mínimo Múltiplo Comum (MMC) e do Máximo Divisor Comum (MDC) são semelhantes? Existem alguns métodos para encontrar o MMC e o MDC, mas ambos podem ser resolvidos através da fatoração. Então por que não utilizarmos um único cálculo para determinar, simultaneamente, o MMC e o MDC? Através de alguns exemplos, vamos demonstrar como isso pode ser feito!

Primeiramente, você lembra como é realizada a fatoração de dois ou mais números? 

No 1° passo, fazemos um grande traço vertical. À esquerda desse traço colocamos os números que desejamos fatorar e, à direita, escrevemos o menor número primo que divide algum dos números que estão à esquerda. 

No 2° passo, tentamos dividir os números à esquerda por aquele que está à direita. Se o número for divisível, colocaremos seu quociente na linha de baixo; se não for, repetiremos o mesmo número na linha inferior. Repetimos esse processo até que restem apenas números “1” no lado esquerdo do traço. 

Observe a seguir a fatoração de 10, 12 e 15:

Processo para efetuar a fatoração de três números

Para calcular o mínimo múltiplo comum entre 12, 15 e 30, basta multiplicar os números que apareceram à direita do traço:

MMC (12, 15, 30) = 2 . 2 . 3 . 5 = 60

Para calcular o máximo divisor comum entre 12, 15 e 30, devemos ver qual foi o número à direita do traço que dividiu todos os números à esquerda de uma vez só. Nesse caso, apenas o número 3 dividiu todos os números, então:

MDC (12, 15, 30) = 3

 Veja outros exemplos de fatoração para realizar o cálculo do MMC e MDC simultaneamente:

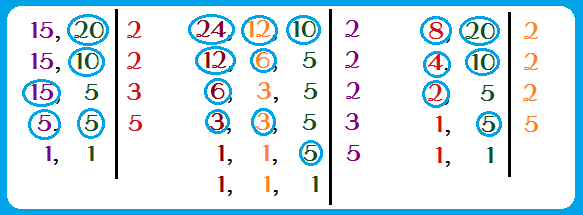
Observe a fatoração para determinar o MMC e o MDC dos números acima

Através da fatoração de 15 e 20, encontramos o MMC (15, 20) = 2. 2. 3. 5 = 60 e o MDC (15, 20) = 5, pois apenas o número 5 divide os dois números. 

Fatorando 24, 12 e 10, encontramos o MMC (24, 12, 10) = 2. 2. 2. 3. 5 = 120 e o MDC (24, 12, 10) = 2. 

Analogamente, podemos verificar que o MMC (8, 20) = 2. 2. 2. 5 = 40 e o MDC (8, 20) = 2. 2 = 4, pois o 2 divide ambos os números duas vezes.

EXERCÍCIOS PROPOSTOS:

01. Encontre os múltiplos positivos dos números abaixo:

a) 8

b) 32

c) 50

d) 100

02. Encontre os divisores positivos dos números abaixo:

a)8

b)12

c) 20

d) 50

03. Calcule os MMC e MDC dos números abaixo:

a) 8,12

b) 15, 45

c) 20,50

d) 60, 100

04.  Aprendiz de Marinheiro - 2016

Seja A = 120, B = 160, x = MMC (A,B) e y = MDC (A,B), então o valor de x + y é igual a:

a) 460
b) 480
c) 500
d) 520
e) 540

Obs: Nas questões abaixo primeiro diga se ela é de MMC ou de MDC e após faça o calculo: 

05. Dois irmãos moram juntos e costumam fazer longas viagens em seus trabalhos. João é maquinista de trem e fica sempre 20 dias fora de casa a cada viagem, folgando no vigésimo primeiro dia. Antônio é piloto de avião e ausenta-se de sua casa por oito dias, tendo o nono dia para descansar. Se ambos os irmãos iniciaram uma viagem hoje, daqui a quantos dias eles poderão encontrar-se em casa?

06. (UEL) Três ciclistas percorrem um circuito saindo todos ao mesmo tempo, do mesmo ponto, e com o mesmo sentido. O primeiro faz o percurso em 40 s, o segundo em 36 s e o terceiro em 30 s. Com base nessas informações, depois de quanto tempo os três ciclistas se reencontrarão novamente no ponto de partida?

07. Sobre uma mesa, há determinado número de planilhas que serão colocadas em pastas, de modo que cada pasta fique com o mesmo número de planilhas. Em cada pasta, é possível colocar 15 planilhas, ou 18 planilhas, ou 20 planilhas, e qualquer que seja a opção, não restará planilhas fora das pastas. O menor número de planilhas que há sobre essa mesa é?

 PORCENTAGEM COM ACRÉSCIMOS E DECRÉSCIMOS SIMPLES:


LINKS PARA ESTUDO DE ACRÉSCIMOS E DECRÉSCIMOS SIMPLES:

https://www.youtube.com/watch?v=nUgAGtEBleM
https://www.youtube.com/watch?v=sXO09XnTyO0
https://www.youtube.com/watch?v=Z8_LS8siQpk

 EXERCÍCIOS RESOLVIDOS:

01. João quer comprar um notebook. Ao chegar na loja viu que o preço era R$ 1800,00 reais. O vendedor afirmou que se ele comprar a vista teria 20% de desconto. Qual o valor que João pagou no notbook a vista?

RESOLUÇÃO:

20% DE 1800 =

20 / 100 X 1800 =

2 / 10 X 1800 =

2 / 1 X 180 =  360

R = 1800 - 360 = 1440,00


EXERCÍCIOS PROPOSTOS:

01. Ricardo trabalha em uma fábrica de tijolos e em janeiro produziu 2500 tijolos. No próximo mês ele teve um aumento de 30% na produção. Quantos tijolos ele produziu em fevereiro?





02. Levi acertou 60% das questões da prova. Sabendo que a prova teve 150 questões. Quantas questões ele acertou?





03.  Beatriz ganhava R$ 1.800,00 reais de salário. Devido a crise ela teve um diminuição de 40% do salário. Qual é o novo salário dela?





04. Pedro percorreu 420 quilómetros em sua viagem de férias. Sabendo que com 50% do percurso ele parou para lanchar e com 70% do percurso ele parou para almoçar. Indique o quilómetro que Pedro parou para lanchar e para almoçar?