MATEMÁTICA – 6ª SEMANA
ANO/SEGMENTO:
8º
Ano/ Anos Finais
COMPONENTE
CURRICULAR: Matemática
UNIDADES
TEMÁTICAS: Números / Probabilidade e estatística.
OBJETOS DE CONHECIMENTO:
I) O princípio
multiplicativo da contagem;
II) Princípio
multiplicativo da contagem Soma das probabilidades de todos os elementos de um
espaço amostral.
HABILIDADES:
(EF08MA03) Resolver e elaborar problemas de contagem cuja
resolução envolva a aplicação do princípio multiplicativo.
(EF08MA22) Calcular a probabilidade de eventos, com base na
construção do espaço amostral, utilizando o princípio multiplicativo, e
reconhecer que a soma das probabilidades de todos os elementos do espaço
amostral é igual a 1.
DESENVOLVIMENTO DO PLANO:
PRINCÍPIO MULTIPLICATIVO DA CONTAGEM:
Objetivo: Elaborar
e resolver problemas de contagem relacionando o principio multiplicativo da
contagem com do diagrama da árvore.
Observe o exemplo resolvido abaixo:
Observe a mais um exemplo resolvido:
Carolina montou seu diagrama da árvore
Conclusão:
Observe a mais um exemplo resolvido:
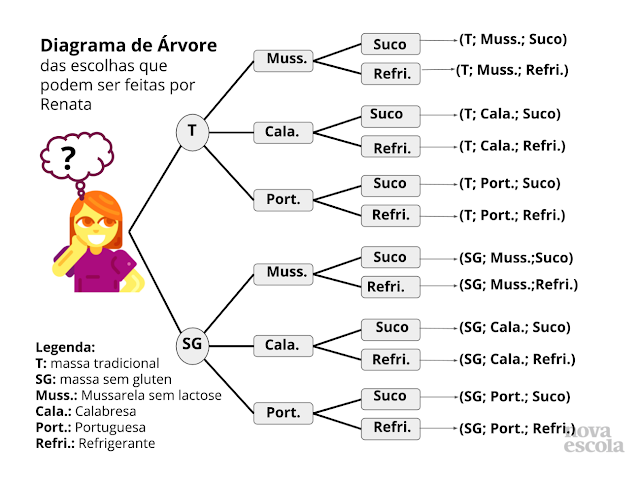
Renata montou seu diagrama da árvore:
Conclusão:
No principio multiplicativo da contagem sabemos de antemão as combinações de pizzas que podem ser elaboradas com os elementos disponíveis, multiplicamos o numero de escolhas que podemos fazer para cada etapa: 2 x 3 x 2 = 12.
Podemos concluir com os exemplos resolvidos
até aqui que:
Principio multiplicativo da contagem: Se uma decisão d1 pode ser tomada de n modos e qualquer que seja esta escolha, outra decisão d2 puder ser tomada de m modos, o número de maneiras de se tornarem consecutivas as decisões d1 e d2 é igual a m x n.
Atividade 01: Aluno resolve
André tem uma pastelaria que vende 5 tipos de
pateis, 3 tipos de sucos e 2 tipos de sobremessa. Faça as combinações possíveis,
utilizando o diagrama da árvore. Faça o calculo da quantidade de combinações.
Solução:
Objetivo: Aplicar
o principio multiplicativo na determinação de elementos de um espaço amostral
Definições:
Espaço amostral: É
conjunto estabelecido por todos os possíveis resultados de um experimento.
Por exemplo:
No lançamento de uma moeda seu espaço amostral
seria cara ou coroa.
No lançamento de um dado o espaço amostral
seriam os números 1, 2, 3, 4, 5 e 6.
Evento: É um conjunto de resultados
do experimento.
Por exemplo:
No lançamento de uma moeda os resultados seriam:
Cara, Coroa ou Coroa, Cara = 2 soluções (eventos).
Probabilidade:
Def: É uma área de
estudo na matemática que permite calcular as chances de um evento ocorrer em um
experimento aleatório.
Exemplo Resolvido:
01. Qual a probabilidade no lançamento de uma moeda dar cara?
Solução:
P = 1 / 2 = 0,5.
Na fração o número 1 representa o que ele
quer que aconteça ( cara ).
Na fração o número 2 representa a
quantidade do espaço amostral.
Atividade 01: Aluno resolve
Solução:
Atividade 02: Aluno resolve
Ana fez o lançamento de um dado e gostaria de
saber:
a)
Qual o espaço amostral? Quantos
elementos possui?
b)
Qual a probabilidade de sair um 2?
c)
Qual a probabilidade de sair um 6?
d)
Qual a probabilidade de sair um 8?
Solução:
Objetivo: Reconhecer
que a soma das probabilidades de todos os elementos do espaço amostral é igual
a 1.
Vamos fazer a demostração desse objetivo com
um exemplo resolvido.
Exemplo resolvido:
Beatriz lançou uma moeda e gostaria de saber
qual a probabilidade de dar cara e depois coroa, assim como ela gostaria de
saber qual a soma das duas probabilidades.
Solução:
Cara = ½ = 0,5
Coroa = ½ = 0,5
A soma das probabilidades seria cara +
coroa, ou seja:
Cara = 0,5 ; Coroa = 0,5; Então: 0,5 + 0,5 = 1
Conclusão:
A soma das probabilidades de qualquer
evento sempre dará 1.
Atividade 03: Aluno resolve
01. Encontre as probabilidades de todos os números no lançamento de um dado
e ao final faça a soma dessas probabilidades.
Solução:








Nenhum comentário:
Postar um comentário