MATEMÁTICA - 7ª e 8ª SEMANA - PROF: STÊNIO AGUIAR - 8º ANOS

MATEMÁTICA – 7ª / 8ª  SEMANA

ANO/SEGMENTO: 8º Ano/ Anos Finais

COMPONENTE CURRICULAR: Matemática

UNIDADE TEMÁTICA: Grandezas e medidas.

OBJETOS DE CONHECIMENTO:

I)   Medidas de capacidade;

II)  Volume de bloco retangular.

HABILIDADES:

(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.

(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.

DESENVOLVIMENTO DO PLANO:

Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes:

LINKS PARA ESTUDO:

https://www.youtube.com/watch?v=3aKysn3tN8c

https://www.youtube.com/watch?v=o8rbkq0yDZE

https://www.youtube.com/watch?v=COr2BhjWmrk

https://www.youtube.com/watch?v=7AOrLZaSicU

https://www.youtube.com/watch?v=BfhlPkRVSLM

https://www.youtube.com/watch?v=o2s8aNnjdzo

https://www.youtube.com/watch?v=j7R4YuLyJ1I

Relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico:

Sempre que fazemos a relação entre grandezas temos algumas observações importantes que serão úteis na resolução das questões.

No 6º ano aprendemos a relação entre grandezas e aprendemos também a fazer a transformação entre essas grandezas como por exemplo:

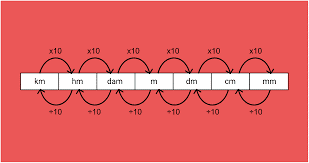
Na transformação de 1 km em metros, qual o valor encontramos? Podemos ver a baixo a relação de transformação.

Podemos concluir que 1 km tem 1000 metros, pois andamos 3 casas de km para m, ou seja multiplicamos cada casa por 10, dando como resultado 10 x 10 x 10 = 1000.

Quando queremos falar em volume temos que lembrar que o cálculo do volume será:

a = largura

b = comprimento ou base

c = altura

Se o cálculo é de um cubo, temos que lembrar que em um cubo todos os lados são iguais ou seja:

Vamos agora para a seguinte situação:

Temos uma caixa d’agua na forma de um cubo e sua capacidade total, ou seja seu volume é de 1000 litros e cada lado dessa caixa d’agua vale 1 metro, podemos concluir que:

Volume = base ou comprimento x largura x altura

Volume = 1m x 1m x 1m (vamos multiplicar os números e as letras)

Obs: Na multiplicação de potencias de mesma base, repete a base e soma os expoentes.

m¹ x m¹ x m¹ = m¹⁺¹⁺¹ = m³

Volume = 1 m³ 

Podemos concluir que o volume é de 1 m³ , mas como a questão já tinha informado que o volume era de 1000 litros, então podemos afirmar que:

1 M³ = 1000 L 

Em uma outra situação podemos ter o lado desse cubo valendo 1 dm e seu volume total é de 1 litro. Vamos observar a ilustração:

Volume = base ou comprimento x largura x altura

Volume = 1 dm x 1 dm x 1 dm

Volume = 1 dm ³

Na questão foi informado o volume como sendo de 1 litro e no nosso calculo podemos concluir que o volume foi de 1 dm ³.

Conclusão:

1 DM ³ = 1 L

Resumo:

• 1 M³ = 1000 L
• 1 DM ³ = 1 L

Atividade 01 resolvida: Professor resolve.

Em uma piscina no formato de um cubo cada lado vale 5 m. Encontre o seu volume e sua capacidade em litros.

Resolução:

Volume = Comprimento ou base x largura x altura

Volume = 5 m x 5m x 5m

Volume = 125 m³

Para o calculo da capacidade em litros temos que fazer a seguinte relação:

1 m³ = 1000 litros, então:

125 m³ = 125 x 1000 = 125.000 litros.

Atividade 02 resolvida: Professor resolve.

Em uma caixa d’agua na forma cúbica, cada lado vale 20 dm. Qual o seu volume em litros?

Resolução:

Volume = Comprimento ou base x largura x altura

Volume = 20 dm x 20 dm x 20 dm

Volume = 8.000 dm³

Para o cálculo da capacidade em litros temos que fazer a seguinte relação:

1 dm³ = 1 L, então:

8.000 dm³ = 8.000 x 1 = 8.000 litros.

Atividade 03: Aluno resolve.

a) Na casa de Roberta tem um aquário na forma de um cubo cujo o lado mede 3 metros. Calcule o volume desse aquário em litros?

Resolução:

b) E se esse aquário tivesse o lado de 30 dm, qual seria seu volume em litros?

Resolução:

Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular:

Quando trabalhamos o volume de qualquer figura geométrica o cálculo é o produto do comprimento ou base, com a largura e com a altura, ou seja:

V = Comprimento ou Base x Largura x Altura

Nas questões anteriores trabalhamos somente com o cubo. Nas próximas questões trabalharemos com um bloco retangular.

Volume = a x b x c

a = Comprimento ou Base

b = largura

c = altura

Lembrando das transformações anteriores:

1 M³ = 1000 L

1 DM ³ = 1 L

Atividade Resolvida 01: Professor Resolve. 

Marcelo construiu uma piscina no formato de um bloco retangular de 2 m de comprimento por 3 metros de largura, por 4 metros de altura.

a) Qual o volume dessa piscina em litros?

Resolução:

V = comprimento ou base x largura x altura

V = 2 m  x  3 m  x  4 m

V = 24 m³

Sabemos que 1 m³ = 1000 litros, então temos:

V = 24 m³ = 24 x 1.000 = 24.000 litros

Atividade 02: Aluno Resolve

Fernanda tem em sua residência uma piscina cujo formado é um bloco retangular de 2 x 4 x 1,60 m. Quando faz a limpeza da piscina ela precisa repor a água em 1/6 do volume total da piscina. Quantos litros de água ela repor na piscina?

Atividade 03: Aluno Resolve

Responda de acordo com o que você aprendeu sobre a matéria:

a)    Em 1 dm³ temos ________ litro

b)    Em 1 m³ temos   ________ litro

c)    Em um cubo seus lados são _______

d)    No volume de um cubo, o cálculo é feito como: ______________

e)    No volume de um bloco retangular, o cálculo é feito como: ___________

Atividade 04: Aluno Resolve

Em um cubo temos que o lado mede 20 metros. Encontre o volume desse cubo em litros.

Atividade 05: Aluno Resolve

Em um bloco retangular, suas medidas são: 30 x 20 x 10 dm. Encontre o volume em litros.