MATEMÁTICA – SEMANA (26, 27, 29 e 30) DE OUTUBRO
ANO/SEGMENTO: 7º Ano/ Anos Finais
COMPONENTE CURRICULAR: Matemática
UNIDADE TEMÁTICA: Números.
OBJETOS DE CONHECIMENTO: Números racionais na representação
fracionária e na decimal: usos, ordenação e associação com pontos da reta
numérica e operações.
HABILIDADE: (EF07MA12) Resolver e elaborar problemas que
envolvam as operações com números racionais.
DESENVOLVIMENTO DO PLANO:
Operações
com números racionais:
Adição e Subtração
Para simplificar a escrita, transformamos a adição e subtração em
somas algébricas. Eliminamos os parênteses e escrevemos os números um ao lado
do outro, da mesma forma como fazemos com os números inteiros.
Exemplo 1: Qual é a soma:
Exemplo 2: Calcule o valor da expressão:
Multiplicação e divisão
Na multiplicação de
números racionais, devemos multiplicar numerador por numerador, e denominador
por denominador, assim como é mostrado nos exemplos abaixo:
Na divisão de
números racionais, devemos multiplicar a primeira fração pelo inverso da
segunda, como é mostrado no exemplo abaixo:
Potenciação e radiciação
Na potenciação,
quando elevamos um número racional a um determinado expoente, estamos elevando
o numerador e o denominador a esse expoente, conforme os exemplos abaixo:
Na radiciação, quando aplicamos a raiz quadrada a um número racional, estamos aplicando essa raiz ao numerador e ao denominador, conforme o exemplo abaixo:
ATIVIDADES PROPOSTAS: O ALUNO RESOLVE
1) Qual é o quociente? Dê o resultado em forma de fração.
a) (+7) : (-2)=
b) (-9) : (+4)=
c) (+22) : (+6)=
d) (-8) : (-4)=
2) Coloque na forma de fração:
a) -1,5=
b) 31,47=
c) -918,5=
3) Qual é maior:
a) 3/5 ou 2/3
b) 4/3 ou 13/10
4) Qual é o menor:
a) - 7/4 ou -9/5
b) - 17/5 ou - - 67 /20
5) Qual é a soma:
a) ( + 3/5) + ( - 7/5) =
b) (- 3/2) + (+5/7) =
c) (+0,3) + (- 0,7) =
6) Qual o produto?
a) (+4/5) x (- 10/3) =
b) (-6/35) x (+25/12) =
7) Calcule:
a) (-4/5) : (-8/7) =
b) (-5/3) : (+ 10/9) =
8) Represente cada número racional por um número decimal. (Divida o numerador pelo denominador da fração).
a) 1/2 =
b) 1/4 =
c) 3/5 =
d) 47/100 =
9) O numeral decimal 0,125 pode ser escrito na forma de fração como:
10) Calcule a potência:
a) (+2)4 =
b) (- 3)5 =
c) 06 =
d) (+8)2 =
e) (-5)2 =
f) (-6)3 =
g) (+5)4





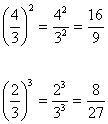

Nenhum comentário:
Postar um comentário