25 maio, 2020

MATEMÁTICA - 3ª SEMANA - PROF: STÊNIO AGUIAR - 8º ANOS

MATEMÁTICA – 3ª SEMANA
ANO/SEGMENTO: 8º Ano/ Anos Finais


COMPONENTE CURRICULAR: Matemática.


UNIDADES TEMÁTICAS: Álgebra / Grandezas e medidas

OBJETOS DE CONHECIMENTO:



  • Valor numérico de expressões algébricas; 
  • Área de figuras planas.

HABILIDADES:

(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.

(EF08MA19 - adaptada) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros e triângulos), em situações como determinar medida de terrenos.




DESENVOLVIMENTO DO PLANO:



LINKS PARA VALOR NUMÉRICO DE EXPRESSÕES ALGÉBRICAS:


  • https://www.youtube.com/watch?v=j3Kx9firjV0

  • https://www.youtube.com/watch?v=o03XxDp9Y7s

  • https://www.youtube.com/watch?v=gYO7o1jothM 

     

    INTRODUÇÃO:




    Observe os dois tipos de expressões matemáticas:

    Expressões Numéricas
    Expressões Algébricas
    a) 7 - 1 + 4
    a) x + y – z
    b) 2 . 5 + 3
    b) 2x – 4a + 1
    c) 82 – 1 + 4
    c) 3x2 – 5x + 9



    Expressões Numéricas - possuem apenas números

    Expressões Algébricas – possuem números e letras ou apenas letras



    Valor Numérico de uma expressão Algébrica



    Para obter o valor numérico de uma expressão algébrica você deve proceder do seguinte modo:



    1º) Substituir as letras por números reais dados.
    2º) Efetuar as operações indicadas, devendo obedecer à seguinte ordem:


    a) potenciação
    b) divisão e multiplicação
    c) adição e subtração



    IMPORTANTE!

    Convém utilizar parênteses quando substituir números negativos.

    Exemplo 1


    Calcular o valor numérico de 2x + 3ª para x = 5 e a = - 4.
    Solução:


    Vamos trocar x por 5 e a por – 4.


    Veja: 2x + 3a = 2 . 5 + 3 . (- 4)
    = 10 + (- 12)
    = 10 – 12
    = - 2





    Exemplo 2
    Calcular valor numérico de x2 – 7x + y para x = 5 e y = - 1


    Solução:
    x2 – 7x + y = 52 – 7 . 5 + ( -1)
    = 25 – 35 -1
    = 25 – 36
    = - 11







    EXERCÍCIOS PROPOSTOS:

    01. Sabendo que x = 4, determine o perímetro do polígono:




    a) 81
    b) 79
    c) 78
    d) 86


    02. Sendo a = 4 e b = - 6, encontre o valor numérico das seguintes expressões algébricas:
    a) 3a + 5b
    b) a2 - b
    c) 10ab + 5a2 – 3b









    03. Consideremos P = 2A+10 e tomemos A = 5. Encontre o valor de P:









    04. Seja X = 4A+ 2 + B - 7 e tomemos A = 5 e B = 7. Encontre X:









    05. Seja Y= 18 – C + 9 + D + 8C, onde C = - 2 e D = 1. Encontre Y:



      



    ÁREAS DE FIGURAS PLANAS:



    LINKS PARA ESTUDO DE ÁREAS DE FIGURAS PLANAS:

  • https://www.youtube.com/watch?v=VxNj6Nuhq1o
  • https://www.youtube.com/watch?v=2_13kTn5xbs
  • https://www.youtube.com/watch?v=p3yJ680N8aE
  • https://www.youtube.com/watch?v=TmJ8fHEg_X0



Definições:

As áreas das figuras planas medem o tamanho da superfície da figura. Desse modo, podemos pensar que quanto maior a superfície da figura, maior será sua área.

Principais Figuras Planas:



Antes de apresentar as fórmulas das áreas das figuras planas, devemos atentar para cada uma delas:

Triângulo: polígono formado por três lados. São classificados de acordo com as medidas dos lados, bem como seus ângulos:

Quanto a medida dos lados:
Quanto a medida dos ângulos:
  • Triângulo Retângulo: possui um ângulo interno de 90°;
  • Triângulo Obtusângulo: possui dois ângulos agudos internos, ou seja, menor que 90°, e um ângulo obtuso interno, maior que 90°;
  • Triângulo Acutângulo: possui três ângulos internos menores que 90°.

Quadrado: quadrilátero regular formado por quatro lados congruentes (mesma medida). Ele é formado por quatro ângulos internos de 90°, os quais são chamados de ângulos retos.



Retângulo: quadrilátero formado por quatro lados, dois deles na vertical e dois na horizontal. Da mesma forma que o quadrado, ele apresenta quatro ângulos internos de 90° (retos).



Círculo: Figura plana também chamada de disco. Apresenta uma forma circular. O raio do círculo representa a medida entre o ponto central da figura e uma das extremidades.
Já o diâmetro equivale duas vezes o raio, posto que representa o segmento de reta que passa pelo centro do círculo, dividindo-o em duas metades iguais.



Trapézio: quadrilátero notável com dois lados e bases paralelas, donde uma é maior e outra menor. A soma de seus ângulos internos totaliza 360°. São classificados em:
  • Trapézio Retângulo: apresenta dois ângulos de 90º (ângulos retos);
  • Trapézio Isósceles: também chamado de trapézio simétrico donde os lados não paralelos possuem a mesma medida;
  • Trapézio Escaleno: todos os lados apresentam medidas diferentes.



Losango: quadrilátero equilátero formado por quatro lados iguais. Apresenta dois lados e ângulos opostos congruentes e paralelos, com duas diagonais que se cruzam perpendicularmente. Ele possui dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º).

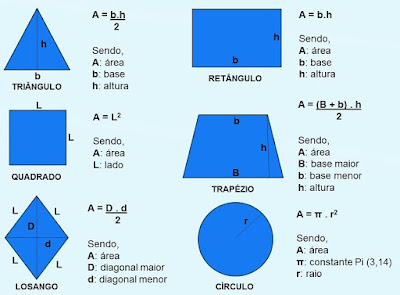
Fórmula das Áreas das Figuras Planas:




Confira abaixo as fórmulas para os cálculos de área:

Atenção!

Vale lembrar que a área e o perímetro são dois conceitos utilizados na geometria plana, no entanto, apresentam diferenças.
  • Área: tamanho da superfície da figura. O valor da área será dado sempre em cm2, m2 ou km2.
  • Perímetro: soma de todos os lados da figura. O valor do perímetro será dado sempre em cm, m ou km. 


    Exercícios Resolvidos:

    01. Considere um trapézio onde a base menor mede 5 cm, a maior 8 cm e altura de 3 cm. Calcule a área desse trapézio.

    Fórmula da área do trapézio:

    A = ((B + b) x h) / 2

    Sabendo que:

    B= 8 cm
    b = 5 cm
    h = 3 cm

    Resolução:
    A = ((8 + 5) x 3) /2
    A = ((13 x 3) /2
    A = 39 / 2
    A = 19,5 cm



    02. Sabendo que o lado do quadrado vale 9 metros. Encontre a área:

    A = L x L = L2
    A = 92 = 81 m2



    03. Em um retângulo a base vale 10 cm e a altura vale 5 cm. Encontre a área:

    A = B (base) x H (altura)
    A = 10 x 5 = 50 cm2


    04. Um triângulo apresenta as seguintes medidas.

    Base = 12 cm
    Altura = 5 cm

    A = ( B x H ) / 2
    A = ( 12 x 5 ) / 2
    A = 60 / 2
    A = 30 cm2




    05. Em um losango encontramos as seguintes medidas:

    Diagonal maior (D) = 20 cm
    Diagonal menor (d) = 12 cm


    A = (D x d) / 2
    A = (20 x 12) / 2
    A = 240 / 2
    A = 120 cm2



    Exercícios Propostos:

    01. Calcule a área de um canteiro de flores em formato de losango, que possui diagonal maior medindo 10 metros e diagonal menor medindo 5 metros.









    02. Um empresário possui um espaço retangular de 110 m por 90 m para eventos. Considerando que cada metro quadrado é ocupado por 4 pessoas, a capacidade máxima de pessoas que esse espaço pode ter é:
    a) 32.400
    b) 34.500
    c) 39.600
    d) 42.500
    e) 45.400





    03. Um trapézio tem a base menor igual a 2, a base maior igual a 3 e a altura igual a 10. Qual a área deste trapézio?












    04. Sabendo que a área de um quadrado é 36cm², qual é seu perímetro?









    05. Calcule a área e o perímetro (em metros) dos retângulos descritos:
    a) a = 25 e b = 12
    b) a = 14 e b = 10









Postado por às

2 comentários:

Assinar: Postar comentários (Atom)