MATEMÁTICA
– 2ª SEMANA
ANO/SEGMENTO:
7º Ano/ Anos
Finais COMPONENTE
CURRICULAR:
Matemática UNIDADES
TEMÁTICAS: Números
HABILIDADES:
(EF06MA03) Resolver e elaborar
problemas que envolvam cálculos (mentais ou escritos, exatos ou
aproximados) com números naturais, por meio de estratégias
variadas, com compreensão dos processos neles envolvidos com e sem
uso de calculadora.
(EF06MA13) Resolver e elaborar
problemas que envolvam porcentagens, com base na ideia de
proporcionalidade, sem fazer uso da “regra de três”, utilizando
estratégias pessoais, cálculo mental e calculadora, em contextos de
educação financeira, entre outros.
OBJETOS DE CONHECIMENTO:
- Operações (adição, subtração, multiplicação, divisão e potenciação) com números naturais. Divisão euclidiana;
- Cálculo de porcentagens por meio de estratégias diversas, sem fazer uso da “regra de três”.
DESENVOLVIMENTO DO PLANO:
Exercício
1.
Efetue
as seguintes adições:
a)110
+ 251. b)225 + 312.
c)763 + 249.
d)1.258 + 2.407. e)27 +319
Exercício
2:
Efetue
as
seguintes
subtrações:
a)379
− 125.
b)432 − 321.
c)1.278 − 1.154. d)411 − 277. e)1.007 −
328.
Exercício
3:
Efetue:
a)234
x2. b)129
x6. c)23 x21.
d)341 x37.
Exercício
4.
Determine
o
quociente:
a)44
: 2. b)69 :
3. c)72 : 4.
d)144 : 6.
Exercício
5.
Quando
Júlia
tinha 7 anos, seu pai tinha 33 anos. Se
hoje ela tem 11 anos, qual a soma da sua idade com a de seu
pai?
Exercício
6.
A
soma de
dois números
e´
75. Se
um deles e´
31, qual
e´
o outro?
Exercício
7.
Qual
a soma
de todos
os números
de três
algarismos que podem ser formados com os algarismos
1, 5 e
6?
Exercício
8.
Telma
comprou uma boneca,
usando 50 reais. Se o troco foi 13 reais, quanto custou a boneca?
Exercício
9.
Jonas
nasceu em 1992. Quantos anos tinha em 2011?
Exercício
10.
Em uma partida de basquete,
os
”Abelhas”
venceram
os
”Legumes” por
uma diferença de
19
pontos. Se os ”Abelhas” fizeram 104
pontos, quantos pontos
fizeram os
”Legumes”?
VÍDEO
EXPLICATIVO SOBRE PORCENTAGEM:
Pequena explicação sobre a porcentagem:
Porcentagem
ou percentagem
é usada para calcular descontos, acréscimo de preços, lucros, etc.
É uma fração em que o denominador é igual a 100. O símbolo para
representar uma porcentagem é %
e vem precedido por um número.
Definição:
Ao número p
associamos a razão p⁄100,
ou seja, tomamos p
partes de um todo que foi dividido em 100
partes iguais.
O nome tem origem do latim (per
centum) e quer dizer por cento, ou
seja, uma razão
de base 100. É frequentemente utilizado para cálculos de transações
comerciais, entre outros.
Essas razões com denominadores 100 são
chamadas de razões centesimais,
taxas percentuais
ou, simplesmente, porcentagens.
Porcentagem no dia a dia
Um dos assuntos que caem em vestibulares, dos mais concorridos aos
menos concorridos do país, também aparece frequentemente em
questões do ENEM.
Além disso, sempre vimos nos telejornais
notícias relacionadas, por exemplo: “O
preço da gasolina aumentou 10%”.
Dessa forma, se a gasolina custa 5,00 reais e esta irá sofrer um
reajuste (aumento) de 10%, na matemática escreveremos assim:
10% de 5,00 = 10⁄100
. 5 = 0,50
Ou seja, a gasolina sofrerá um aumento de 50
centavos por litro.
Ao calcularmos uma porcentagem em relação a
um valor dado, estamos também representando uma proporção
em que um dos denominadores é igual a 100.
Pelo exemplo acima dado, dizemos que 0,50 representa em 5 o mesmo que 10 representa em 100. Veja:
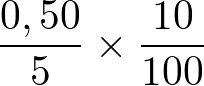
Como representar porcentagem?
Existem três formas de representarmos uma porcentagem: na forma percentual, forma fracionária ou forma decimal. Veja:| Forma percentual | Forma fracionário | Forma decimal |
|---|---|---|
| 10% | 10⁄100 | 0,1 |
| 30% | 30⁄100 | 0,30 |
| 5,3% | 5,3/100 | 0,053 |
Podemos perceber como a porcentagem está presente na nossa vida.
Descontos em lojas, promoções na internet, dificilmente você vai
se livrar do assunto.
Usamos a porcentagem quando queremos expressar alguma quantidade
como a porcentagem de um valor. Veja um exemplo:
Digamos que você vai em uma loja no shopping ou numa loja virtual
na internet e encontre um produto com desconto de 10%. Seu custo
inicial era de R$ 50,00. Esse desconto de 10% corresponde à divisão
do preço inicial por 100, tomando 10 partes. Veja:
Resumindo: calcular a porcentagem de a%
de x
é o mesmo que multiplicar a/100
por x.
Entender porcentagem é fundamental para o dia
a dia. Se você for a um posto de combustível abastecer seu carro,
após ouvi na televisão que a gasolina teve tantos por cento de
aumento e, digamos que seu carro seja flex, então você para e
pensa: “devo abastecer com álcool ou
gasolina? Quantos por cento devo abastecer de álcool ou gasolina?”.
São problemas como esse que nos deparamos e percebemos que a
porcentagem é muito importante em nossa vida.
ATIVIDADES SOBRE PORCENTAGEM:
OBS:
CALCULE AS PORCENTAGENS SEM FAZER A REGRA DE TRÊS
Questao
01:
Passe
da linguagem formal para a forma matemática:
a)
20 por cento de 50
Resolução:
20/100
x 50 (Forma matemática)
b)
30
por cento de 70
c)
60 por cento de 150
d)
15 por cento de 230
Questão
02:
Calcule
as porcentagens abaixo:
a)
20% de 60
Resolução:
20/100
x 60 (cortamos os zeros do numerador e do denominador)
2/10
x 60 (multiplicamos o número
2 com o número
60 que dá igual a 120)
120/10
(dividimos o 120 por 10 que dá 12)
R
= 12
b)
30% de 120
c)
40% de 200
d)
70% de 300
e)
90% de 420
f)
50% de 50
Questão
03:
Obs:
Utilizando o mesmo método da questão 2, resolva os problemas a
seguir:
a)
Camila comprou uma sandália que custava R$ 80,00 reais, como ela
comprou a vista, ela ganhou 20% de desconto. Quanto Camila pagou pela
sandália?
Resolução:
20%
de 80
20/100
x 80
2/10
x80
160/10
= R$ 16,00 (desconto)
Como
o desconto foi de R$ 16,00 então temos:
80
(valor da sandália) – 16 (desconto) = R$ 64,00
b)
Rodrigo abasteceu seu carro e deu R$ 230,00 reais como ela pagou em
dinheiro, obteve 30%
de desconto. Quanto ele pagou pelo combustível.
c)
Mario comprou 3 blusas, 2 pares de meias, 1 par de sapato. Sabendo
que cada blusa custou R$ 30,00 reais, cada meia custou R$ 5,00 reais
e o sapato custou R$ 160,00 reais. No final da compra ele ganhou um
desconto de 40%. Quanto ele pagou?
d)
Vicente queria comprar um violão
que custava
R$ 380,00 reais. Como
Vicente demorou para ir comprar o violão, o produto teve um aumento
de 20%. Quanto foi o aumento? Quanto Vicente pagou?
e) Marina acertou 80% da prova. Sabendo que a prova tinha 160 questões. Quantas questões Marina acertou?
Nenhum comentário:
Postar um comentário